
Chapter 4
완전 탐색 - 시뮬레이션/ Brute Force
어떻게든 답을 구한다
완전 탐색
- 모든 경우의 수를 시도한다.
- 문제해결의 가장 기본적인 방법
- 별도의 최적화 없이, 효율성을 고려하지 않는 풀이방법
예) 9 명의 난쟁이의 키가 주어질 때, 키의 합이 100이 되는 일곱 난쟁이를 찾아라.
- 9 난쟁이의 합을 구한 뒤, 두 명의 난쟁이의 키를 빼서 100이 되는 경우를 찾으면 됨
모든 경우의 수를 체계적으로 검사할 수 있도록 설계해야 한다.
- 문제가 요구하는 바를 이해하고, 정확히 구현할 수 있어야 한다.
가장 쉽고 간단한 접근
- 효율을 생각하지 않기 대문에 문제의 크기가 작으면 유용하다.
- 문제의 크기가 클수록 시간/공간복잡도가 늘어나 적용이 어려울 수 있다.
- 완전한 정답이 되지 못하더라도 문제를 이해하거나 테스트케이스를 확인하기 위한 용도로 적용해볼 수 있다.
- 부분점수 문제라면 전체를 풀지 못해도 작은 데이터에 대한 점수를 얻을 수 있다.
- 선형 완전탐색, 비선형 완전탐색 등이 있으나 아직은 선형탐색만
시뮬레이션 : 문제에서 주어진 상황을 그대로 진행하며 해결해보는 기법
- 문제의 요구사항에 알맞은 코드 모델링
- 문제의 조건을 체계적으로 수행하기 위한 구현력이 필요
문제 풀이


유레카 이론 성공다국어
| 1 초 | 256 MB | 13015 | 7576 | 5949 | 57.500% |
문제
삼각수 Tn(n ≥ 1)는 [그림]에서와 같이 기하학적으로 일정한 모양의 규칙을 갖는 점들의 모음으로 표현될 수 있다.
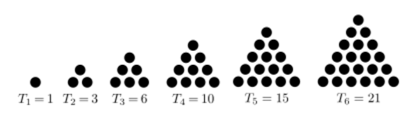
[그림]
자연수 n에 대해 n ≥ 1의 삼각수 Tn는 명백한 공식이 있다.
Tn = 1 + 2 + 3 + ... + n = n(n+1)/2
1796년, 가우스는 모든 자연수가 최대 3개의 삼각수의 합으로 표현될 수 있다고 증명하였다. 예를 들어,
- 4 = T1 + T2
- 5 = T1 + T1 + T2
- 6 = T2 + T2 or 6 = T3
- 10 = T1 + T2 + T3 or 10 = T4
이 결과는 증명을 기념하기 위해 그의 다이어리에 “Eureka! num = Δ + Δ + Δ” 라고 적은것에서 유레카 이론으로 알려졌다. 꿍은 몇몇 자연수가 정확히 3개의 삼각수의 합으로 표현될 수 있는지 궁금해졌다. 위의 예시에서, 5와 10은 정확히 3개의 삼각수의 합으로 표현될 수 있지만 4와 6은 그렇지 않다.
자연수가 주어졌을 때, 그 정수가 정확히 3개의 삼각수의 합으로 표현될 수 있는지 없는지를 판단해주는 프로그램을 만들어라. 단, 3개의 삼각수가 모두 달라야 할 필요는 없다.
입력
프로그램은 표준입력을 사용한다. 테스트케이스의 개수는 입력의 첫 번째 줄에 주어진다. 각 테스트케이스는 한 줄에 자연수 K (3 ≤ K ≤ 1,000)가 하나씩 포함되어있는 T개의 라인으로 구성되어있다.
출력
프로그램은 표준출력을 사용한다. 각 테스트케이스에대해 정확히 한 라인을 출력한다. 만약 K가 정확히 3개의 삼각수의 합으로 표현될수 있다면 1을, 그렇지 않다면 0을 출력한다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
int[] triangleNums = new int[45];
int isExist = 0;
for (int i = 1; i < 45; i++) {
triangleNums[i] = i * (i + 1) / 2;
}
while (T > 0) {
int N = sc.nextInt();
for (int i = 1; i < 45; i++) {
for (int j = 1; j < 45; j++) {
for (int k = 1; k < 45; k++) {
if (triangleNums[i] + triangleNums[j] + triangleNums[k] == N) {
isExist = 1;
break;
}
}
}
}
System.out.println(isExist);
isExist = 0;
T--;
}
}
}
계속 런타임 에러가 나서 무엇인가 했는데 패키지 안 지워서였다. 젠장!
'IT > 알고리즘' 카테고리의 다른 글
| 패스트캠퍼스 Java 코딩테스트 강의 3주차 (0) | 2023.05.02 |
|---|---|
| 카운팅 정렬 (0) | 2023.04.30 |
| 다익스트라 알고리즘 (0) | 2023.04.28 |
| 함수의 점근적 분석법 (0) | 2023.04.28 |
| 패스트캠퍼스 Java 코딩테스트 강의 1주차 (0) | 2023.04.22 |